개요
Hash 충돌에는 다양한 회피 알고리즘이 있습니다. 더 나은 성능을 위해서 계속 성능이 좋은 방식으로 진화하고 있으며, 대표적으로 HashMap에서 사용됩니다. 하지만 항상 최신 방법이 좋은 것은 아니며, 트레이드오프(trde-off)를 잘 따져보고 사용해야 합니다.
목차
Direct-Address Table
Hash & HashTable 이란?
Hash Function 나눗셈 방법
Collision
1. Chaining
2. Open Addressing
- Linear Probing
- Quadratic Probing
- Double Hashing
Open Addressing 성능
Direct-Address Table
Direct-Address Table은 배열을 사용해서 실제 key값이 바로 해당 배열 index에 삽입하는 방식입니다. 즉 key값 = index값 = 해당 배열 값입니다. 하나의 배열 공간에 하나의 값이 유일하게 위치하기 때문에 독립적으로 구분된다는 장점이 있으며 따라서 검색, 삽입, 삭제 모두 O(1)의 시간을 가집니다. Hash 사용 이전에는 Direct Address 방법이 사용되었습니다.
하지만, 최대값이 너무 크다거나, 최댓값에 비해 값이 적어 실제 사용 공간이 많지 않다면 심각한 공간 낭비를 초래합니다. 따라서 공간을 효율적으로 사용하면서, 최대한 유일한 값을 가지며, 배열에 골고루 분포하도록 hash를 사용합니다.
Hash & HashTable 이란?
Hash는 Direct-Address와 달리 hash function을 이용해 key값을 한 번 처리하고 index를 정하는 방식입니다. 이 index에 따른 key 값을 정리해 둔 배열을 hash table이라고 부릅니다. k를 key값, m을 hash table의 크기라 했을 때, 일반적으로 h(k) = k mod m 의 알고리즘을 사용합니다. 좋은 해쉬 함수란 최대한 해쉬 테이블의 각 index마다 값이 중복되지 않고 골고루 key 값이 분배되도록 하는 함수라고 할 수 있다.
Hash Function 나눗셈 방법
일반적인 해쉬 알고리즘은 k mod m 인데, 효율적인 m을 선택하는 방법은 다음과 같습니다.
k의 하위비트를 p라 할 때 m=2^p를 피하는 것입니다.(2의 지수승을 피한다.) 왜냐하면 컴퓨터는 2진수로 표현이 되기 때문에 key값이 어떤 숫자가 되어도 나머지 계산을 하면 key값 전체에 영향을 받는 것이 아니라 항상 key의 맨 뒤의 몇 자리에 영향을 받기 때문입니다.
k = 10110100, m = 0010000, h(k)= 0100
마찬가지로 m=2^p-1도 2의 지수승과 큰 차이없이 비슷한 값이기 때문에 피합니다. 답은 2^p에 너무 가깝지 않은 소수를 선택하는 것입니다. 예를 들어 key값의 개수가 2000이면 해쉬 테이블의 크기를 m=701로 잡습니다. 701은 2000을 3으로 나누었을 때 2의 지수승에 가깝지 않은 소수입니다. h(k) = k mod 701을 사용하면 된다.
Collision
해쉬 함수를 사용하여 index를 만드는 과정에서 대부분 index 중복이 발생합니다. 즉 h(k1) = h(k2)인 상황이 발생합니다. 이 때 "충돌이 발생했다"라고 표현합니다. 배열 공간은 하나인데, 만약 같은 해쉬 값을 가진 2개의 key값을 어떻게 저장해야 할까요? 충돌을 피하는 다양한 해결 방식이 있는데, 대표적으로 Chaining, Open Addressing이 있습니다.
1. Chaining
Chaining은 한 공간당 들어갈 수 있는 갯수를 제한하지 않고 LinkedList로 만들어 계속 key값을 추가하는 방법입니다. 체인은 말그대로 LinkedList로 key값을 계속 연결해 나가기 때문에 붙여진 이름입니다. 유연하게 공간을 사용할 수 있지만 반대로 메모리 문제를 발생시킬 수 있습니다.
다음은 Chaining의 동작 과정입니다.
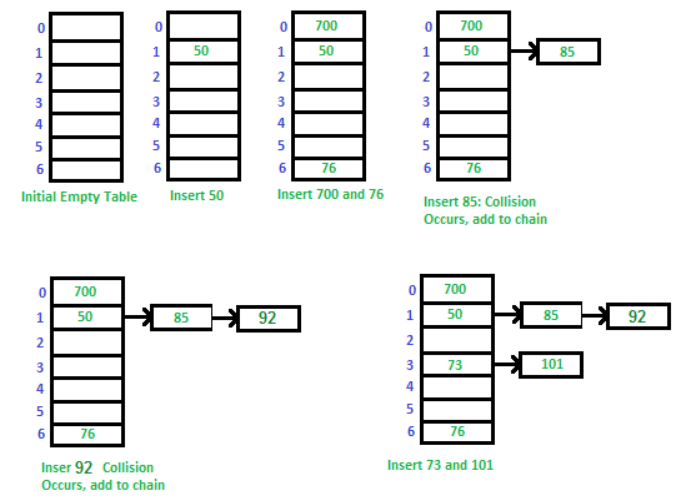
전제조건은 다음과 같습니다.
key 값 : 50 , 700, 76, 85, 92, 73, 101
m 값(배열크기) : 7
일반적인 k mod m 알고리즘을 따르겠습니다.
m = 해쉬테이블에서 사용되는 공간 갯수
n = 해쉬테이블에 입력된 갯수결과는 다음과 같습니다.
적재율 a = m/n
검색,삭제 : O(1+a) [최악 시 O(n)]
삽입 : O(1)
- 장점
적재율이나 해쉬 함수에 대해 별로 신경 쓰지 않아도 되고 구현이 간단합니다.
계속 체인으로 연결하기 때문에 공간사용이 유연하여 해쉬 테이블의 포화상태가 없습니다.
- 단점
사용하지 않고 남는 공간이 있기 때문에 메모리가 낭비됩니다.
체인의 길이가 너무 길어지면 탐색이 O(n)이 되어 해쉬의 장점을 이용하지 못합니다.
LinkedList를 사용하여 저장하므로 캐시의 성능이 저하됩니다.(Open Addressing은 Cache 성능이 좋다.)
2. Open Addressing
Open Addressing은 chaining과 달리 한 공간에 들어갈 수 있는 개수가 제한되어 있어 알고리즘을 반복해 비어있는 공간을 계속 찾는 방법입니다. 메모리를 낭비하지 않지만 해쉬충돌이 일어므로 알고리즘 선택에 주의해야 합니다. 선형 탐사(Linear Probing), 제곱 탐사(Quadratic probing), 이중 해싱(Double Hashing) 총 3가지의 방법이 있습니다.
①선형 탐사(Linear Probing)
h(k, i) = (k+i) mod m

선형탐사(Linear Probing)는 최초 저장되는 공간에 값이 있으면 비어있는 공간이 나올 때까지 1씩 이동하여 탐색합니다. 하지만 primary clustering 문제가 발생하는데, 한 번 충돌하기 시작하면 해당 지역은 계속 충돌이 발생합니다. 위 사진에서 52번에서 충돌이 있어 53,54,55,56까지 이동하고 57까지 이동해서야 비로소 값을 할당합니다. 평균 검색시간이 너무 늘어나기 때문에 hash의 성능을 효율적으로 이용할 수 없습니다.
2. 제곱탐사(Quadratic Probing)
h(k, i) = (h'(k) + c1i+c2i^2) mod m
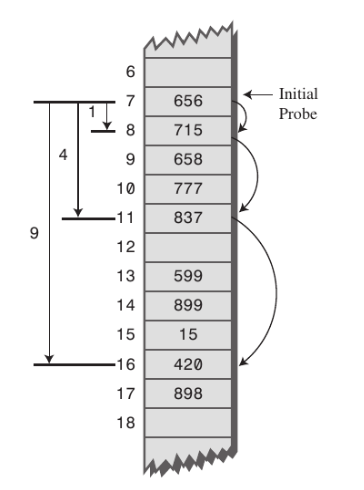
제곱탐사(Quadratic Probing)는 선형 탐사에서 복잡하게 발전된 형태로 상수 c1, c2와 h'(k) 계산을 이용하여 i의 제곱 값으로 탐색하는 방법이다. 하지만 이 방법은 secondary clustering 단점이 있는데 처음에 같은 해쉬값이 나온다면, i값에 따라서 해쉬값이 바뀌기 때문에 선형탐사와 같이 계속 충돌이 반복적으로 발생합니다.
3. 이중 해싱(Double hashing)
h(k,i) = (h1(k) + i*h2(k)) mod m
이중 해싱(Double hashing)은 2개의 해쉬함수를 이용하는 동시에 횟수가 늘어날 때마다 i값을 증가시켜서 독립적인 해쉬값을 가지는 방법입니다. 선형탐사, 제곱 탐사에서 각각 발생하는 primary clustering, secondary clustering의 문제를 모두 해결할 수 있습니다.
해쉬함수에 따라 성능이 달라지는데 h2(k) 함수는 해쉬 테이블 크기 m과 서로소여야 합니다. m을 소수로하고 h2(k)이 m보다 작은 정수이어야 합니다.
h1(k) = k mod 13
h2(k) = 1 + (k mod 11)
h(k,i) = (h1(k) + i*h2(k)) mod 13
Open Addressing 성능
m = 해쉬테이블에서 사용되는 공간 개수
n = 해쉬 테이블에 입력된 개수
a = n/m(적재율)
- 삽입 : O(1/(1-a))
- 조회 : O(1/(1-a))
삭제 시, 주의해야 합니다. 만약 A, B, C가 연속하고 있는 해쉬 테이블에서 B가 삭제되어 A, NULL, C 가 되었고 이때 C를 삭제한다고 가정해보겠습니다.
A가 있는 index부터 쭉 순회를 할 때 중간에 NULL이 있기 때문에 C까지 조회하지 못하고 종료합니다. 왜냐하면 NULL이 입력되지 않고 비어있는 값인지, 삭제되어서 비어있는 공간인지 확인할 수 없기 때문입니다. 따라서 삭제된 공간은 삭제되었다고 DEL과 같이 표시하여 계속 다음 index를 조회할 수 있도록 합니다. A, DEL, C와 같은 형식으로 남겨두면 안정적으로 C까지 조회하고 삭제를 할 수 있습니다.
참고
https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
https://www.geeksforgeeks.org/hashing-set-2-separate-chaining/
'학습' 카테고리의 다른 글
| Interface vs Abstract Class (0) | 2020.08.23 |
|---|---|
| JIT Compiler (0) | 2020.08.16 |
| Iterator & Enumeration & ListIterator (0) | 2020.07.23 |
| Fail-Fast vs Fail-Safe (0) | 2020.07.23 |
| ArrayList & Vector 차이점 (0) | 2020.07.23 |

